4 円及び円弧

4.1 円周及び円弧の等分方法

4.1.1 円弧を2等分する

（1）弧ABの端点A,Bを中心として任意の同一半径の弧を描き、両弧の交点C,Dを求める。

（2）C,Dを結ぶ直線はABの中心を通り、その交点EはABを2等分している。4.1.2 円周を3等分又は6等分する。

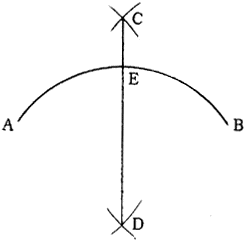
図1.13

4.1.2円周を3等分又は6等分する

（1）円Oにおける円周上の任意の点Aを中心として円Oと同一半径の弧を描き、交点をB,Fとする。

（2）B点より同一半径の弧を描いてCを求め、順次D,Eを求める。A,C,E点は円周を3等分し、A,B,C,D,E,F点は6等分するこれらの等分点を直線で結べば、それぞれ正三角形と正六角形が描ける。

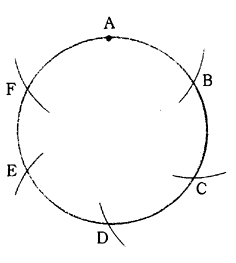
図1.14

4.1.3 円周を任意の数に等分する

（1）直径ABを任意の数に等分する例えば5等分するものとし、その等分点をC,D,E,とする。

（2）A,B点を中心としてABを半径とする弧を描き、両弧の交点をGとする。Gと第2分割点Dとを結ぶ延長線が円周と交わる点をHとすれば、AHは円周を5等分する弧である。

（3）AHを半径とする弧で円周を順次等分すれば、A,H,I,J,Kは円周を5等分する。この方法により、任意の正多角形を描くこともできる。

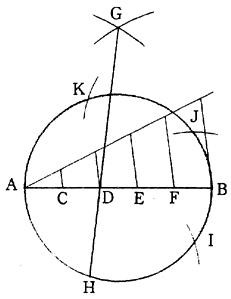
図1.15

前ページ　　　目次へ　　　次ページ